Cores beta de JOTEGO para MiSTerFPGA
Los cores arcade de JOTEGO para FPGA son reconocibles por la marca JT en el menú. Estos cores recrean sistemas arcade con una fidelidad inédita y funcionan en diversas plataformas FPGA, como MiST y SiDi, pero la más famosa en sin duda MiSTerFPGA.
Los cores de JOTEGO se publican cuando están ya maduros pero es posible participar en la fase de prueba beta convirtiéndose en mecenas suyo en Patreon. Los mecenas también pueden acceder a explicaciones del desarrollo, cuestiones técnicas y curiosidades sobre los juegos.
Todos los cores de JOTEGO están disponibles en el repositorio JTBIN de GitHub. Este repositorio tiene una carpeta para cada sistema FPGA:
Los sistemas mantenidos al día son MiSTer, MiST, SiDi, NeptUNO, MultiCore2 y MultiCore2+. Hay algunos cores disponibles en versiones antiguas para UnAmiga, ZXDOS y una placa de pruebas de Cyclone 5.
Para todos los sistemas menos MiSTer, sólo están disponibles compilaciones públicas aquí. Sin embargo para MiSTer, también están los cores en beta. Hay una carpeta para cada core y aunque en general es un core por sistema arcade, esto puede resultar un poco confuso. Por ejemplo bubl es el cor para los juegos Tokio y Bubble Bobble. cps1 es el cor para todos los juegos de CAPCOM SYSTEM 1. Pero los juegos de SEGA System 16 utilizan una riada de cores (s16, s16a2, s16b, s16b2, s16b3).
La instalación manual consiste en copiar el último fichero RBF de cada core -llevan codificada la fecha en el nombre- al directorio _Arcade/cores de MiSTer. Ademas de copiar los fichero MRA que hay en la carpeta mra de JTBIN a _Arcade.
Esto puede ser muy engorroso, así que lo mejor es utilizar la utilidad update_all de TheYpsilon. Hay que configurarla para que descargue los juegos en beta, como se ve en este vídeo. Con esa utilidad basta con correrla desde el menú Scripts de MiSTer para obtener todos los ficheros de golpe.
Después de actualizar todos los cores estarán instalados, pero aquellos en fase beta lucirán este mensaje:
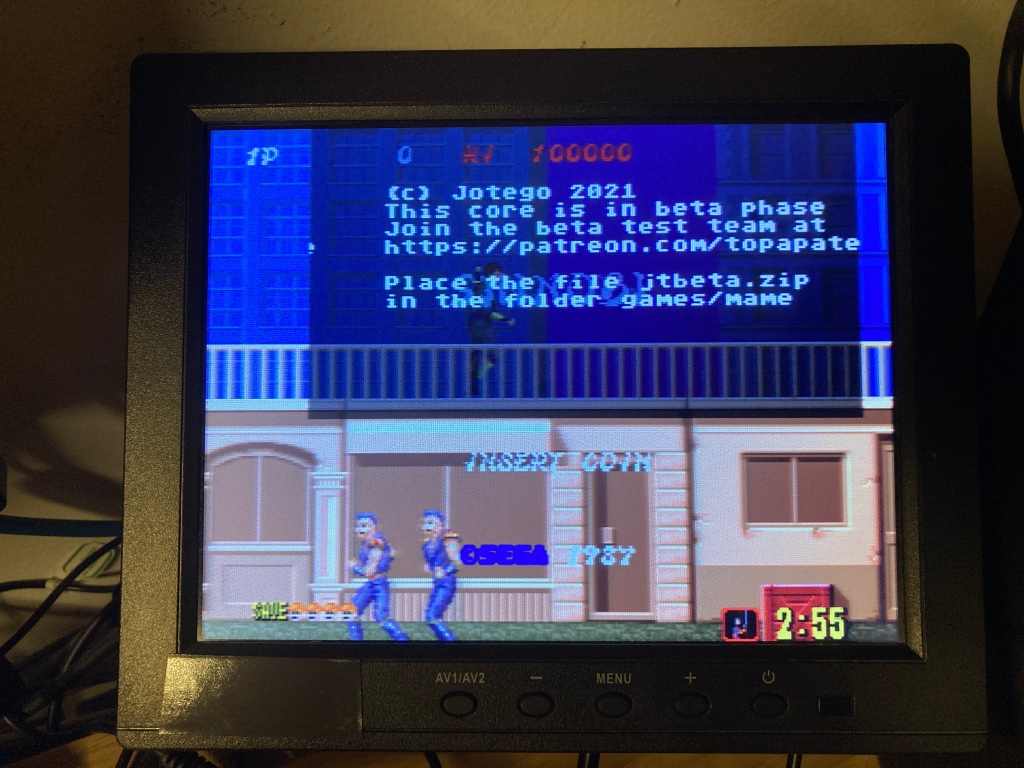
Los juegos en fase beta tienen las entradas bloqueadas y no pueden jugarse si no formas parte del equipo de pruebas beta. Una vez registrado como mecenas en Patreon, podrás jugar gracias a un fichero llamado jtbeta.zip. Este fichero ha de copiarse manualmente al directorio games/mame de la tarjeta SD de MiSTer. Los juegos en beta lo detectan automáticamente y se desbloquean.
¿Dónde está jtbeta.zip?
Este fichero se encuentra en muchos sitios:
- En el canal #betafiles del Discord de JOTEGO. A este Discord se accede enlazando tus cuentas de Patreon y Discord como se explica aquí.
- En la última entrada que haya publicado JOTEGO en Patreon con una beta estará el jtbeta.zip adjunto
- En el repositorio jtbeta de GitHub, disponible para suscriptores por GitHub
- En los ficheros zip con las betas de MiSTer para instalación manual que se adjuntan a las publicaciones de Patreon. En estos archivos zip ya está todo listo para descomprimir directamente a la raíz de la SD y obtenerlo todo en su sitio
- Los mismos archivos zip se obtienen por correo electrónico, si tienes configurado el Patreon para que te lleguen las publicaciones por correo
El fichero jtbeta.zip no hay que descomprimirlo. Sólo se copia y se actualiza ocasionalmente. Puede ocurrir que el fichero cambie mientras un cor todavía está en beta. En ese caso, las versiones más recientes del cor en beta buscarán el nuevo jtbeta.zip y se bloquearán con el antiguo.
JOTEGO publica el código fuente y los binarios de todos sus cores cuando están listos. La fase beta es importante para la calidad y para la continuación del proyecto porque es la principal fuente de financiación del mismo. Por favor no distribuyas el fichero jtbeta.zip y apoya el desarrollo.
Compilar MAME en Ubuntu
Aunque las instrucciones oficiales deberían bastar, a veces no ocurre así. Sobre todo si tienes una instalación mixta de 32 y 64 bits. Y eso es precisamente lo que tienes si has instalado Quartus 13 según mis instrucciones. Así que, qué hacer:
- Obten el código fuente de MAME desde github
- Añade las dependencias
sudo apt-get install git build-essential python libsdl2-dev libsdl2-ttf-dev libfontconfig-dev qt5-default - Selecciona una etiqueta tag en vez de compilar la versión de cabeza
- Define la variable PKG_CONFIG_PATH:
export PKG_CONFIG_PATH=/usr/lib/x86_64-linux-gnu/pkgconfig - Compila explicitando que el código no es seguro
make REGENIE=1 CFLAGS='-U_FORTIFY_SOURCE' - Si falla debido a QT: compila con la versión de QT explícita
make REGENIE=1 CFLAGS='-U_FORTIFY_SOURCE' QT_SELECT=5 QT_HOME=/usr/lib64/qt5
Fíjate que si SOURCES se omite, se compilan todos los drivers. - En mi caso /usr/lib64/qt5 es un enlace simbólico a /usr/lib/qt5
Pista final: si solo te interesa un juego en concreto (por ejemplo, combatsc):
make SOURCES=src/mame/drivers/combatsc.cpp REGENIE=1 CFLAGS='-U_FORTIFY_SOURCE' QT_SELECT=5 QT_HOME=/usr/lib64/qt5
Estas instrucciones me funcionaron en Ubuntu MATE 20.04
Curiosidades sobre el arcade 1942 (CAPCOM, 1984)
Estoy convirtiendo los arcades de CAPCOM de la era anterior al Street Fighter II a FPGA. Estos son algunos de los títulos en los que estoy trabajando:
-Ghosts’n Goblins
-1942
-1943
-Avengers
-Black Tiger
-Commando
-Exed exes
-Gun Smoke
-Legendary Wings
-Rush & Crash (aka The Speed Rumbler)
-Section Z
-Side Arms (Forgotten Worlds predecessor)
-Son Son
-Tiger Road
-Trojan
-Vulgus
Ya he acabado los dos primeros de la lista y hoy vengo a hablaros de curiosidades de 1942, y su comparación con Ghosts’n Goblins.
Los objetos (sprites) en pantalla tienen una peculiaridad que los distingue del fondo o del marcador y es que pueden aparecer en cualquier parte: ¡cualquiera! Mientras que los circuitos para hacer el fondo son relativamente sencillos, los objetos necesitan circuitos más complicados y sobre todo, saber de antemano qué objetos van a aparecer en la pantalla.
El procesador rellena la memoria de los objetos antes de cada imagen aprovechando el intervalo de refresco vertical de la imagen. La memoria de los objetos es accesible directamente por el procesador y éste la rellena. En la recreativa 1942 el procesador podía llegar a escribir 128 bytes en ese tiempo, suficiente para 32 objetos. Nunca verás más de 32 objetos en ninguna escena de 1942.
Pero para Ghosts’n Goblins los diseñadores querían más. Y el procesador no podía dar más. Los procesadores no son muy buenos moviendo datos de un sitio a otro. Así que decidieron poner un DMA (acceso directo a memoria) para los sprites. El procesador escribía los datos de los objetos, a su ritmo, y cuando los tenía listos -y sólo durante el refresco vertical- avisaba al circuito de objetos. Este activaba el DMA y copiaba los datos a la máxima velocidad del sistema. Esto explica el tamaño generoso de los objetos en G&G y también lo cara que era la máquina porque todos esos circuitos extra para el DMA eran muy caros en esa época.
En 1942 aparecen aviones muy grandes en pantalla. Para ahorrar memoria en el búfer de los sprites los diseñadores tomaron una extraña decisión: permitir que los objetos pudieran tener un tamaño de 16×16 o 32×16 o 64×16. Así los aviones peqeños gastan un bloque de 16×16 y los más grandes varios bloques de 64×16. Esto en hardware lo hacen con dos bits que el procesador escribe para cada sprite. Ahí elige el tamaño. Luego el hardware pinta más o menos líneas según esos bits. La verdad es que es una decisión que aunque sea inteligente no tengo muy claro que realmente fuera eficiente. En Ghosts’n Goblins no existe esta opción, aunque claro, los monstruos de Ghosts’n Goblins en general no son tan grandes y cuando lo son, están más animados que los aviones de 1942.
Otra curiosidad es que los esquemáticos que circulan por internet de 1942 no parecen realmente corresponder a ese juego. Hay varios detalles que no coinciden con lo que el juego necesita:
- La ROM de sonido en los esquemáticos tiene 8kB, pero realmente ocupaba 16kB.
- Había el doble de ROMs de objetos de lo que se ve en los esquemáticos
- El decodificador de la posición vertical de los objetos no funciona como en los esquemáticos
Otra cosa rara es que el juego usa memorias ROM para las paletas de colores. Me explico, los gráficos en las memorias se graban con un índice para cada color. Por ejemplo, un número de 0 a 7 que indica que color usar para ese píxel. Pero ese color luego se saca de una paleta. Y esas paletas las guarda 1942 en memorias fijas, en ROM. En Ghosts’n Goblins están grabadas en RAM así que el procesador puede cambiarlas según las circunstancias. Hacerlo en RAM es mucho más flexible… ¿por qué no lo hicieron así en 1942? Es más, ¿por qué lo enrevesaron hasta el punto de tener dos niveles de paletas cada uno con sus ROM? No lo sé exactamente, pero sospecho que las memorias RAM serían muy caras en su momento y que la circuitería para conectar a una RAM era más costosa de añadir también.
1942 tiene uno de los sistemas de servicio más completos que he visto. Puedes probar a arrancar el juego en MAME y pulsar F2 (o seleccionar ”service» entre las opciones DIP) y verás un menú muy completo para probar que las distintas partes del sistema funcionan. Si queréis verle las tripas a uno de estos sistemas, la función de servicio de 1942 es un buen sitio para divertirse.
En cuanto al desarrollo, he procurado reaprovechar al máximo el Ghosts’n Goblins. Ahora me queda la tarea de reunir los dos arcades en la misma rama de github. De momento tengo las versiones de MiST y MiSTer, pero quiero añadir ZX-UNO y ZX-DOS también (Antonio Villena y Manuferhi hacen estas placas)
Instalar Altera Byte Blaster I/II en Ubuntu
Altera hizo sus productos pensando en Red Hat, así que cuando usamos otra distribución las cosas a veces no funcionan sin más. Para el Quartus II v13 quería usar un cable Byteblaster baratito. Lo enchufé y parecía que lo reconocía pero fallaba la escritura. Tras buscar un poco en la red profunda encontré esto. Hay que crear dos ficheros en /etc/udev/rules.d y ya está. Esto lo probé con xUbuntu 18.04 LTS.
Ejecuta luego sudo udevadm control –reload para recargar las reglas.
51-usbblaster.rules
# USB-Blaster
BUS=="usb", SYSFS{idVendor}=="09fb", SYSFS{idProduct}=="6001", MODE="0666"
BUS=="usb", SYSFS{idVendor}=="09fb", SYSFS{idProduct}=="6002", MODE="0666"
BUS=="usb", SYSFS{idVendor}=="09fb", SYSFS{idProduct}=="6003", MODE="0666"
# USB-Blaster II
BUS=="usb", SYSFS{idVendor}=="09fb", SYSFS{idProduct}=="6010", MODE="0666"
BUS=="usb", SYSFS{idVendor}=="09fb", SYSFS{idProduct}=="6810", MODE="0666"
92-usbblaster.rules
# USB-Blaster
SUBSYSTEM=="usb", ATTR{idVendor}=="09fb", ATTR{idProduct}=="6001", MODE="0666"
SUBSYSTEM=="usb", ATTR{idVendor}=="09fb", ATTR{idProduct}=="6002", MODE="0666"
SUBSYSTEM=="usb", ATTR{idVendor}=="09fb", ATTR{idProduct}=="6003", MODE="0666"
# USB-Blaster II
SUBSYSTEM=="usb", ATTR{idVendor}=="09fb", ATTR{idProduct}=="6010", MODE="666"
SUBSYSTEM=="usb", ATTR{idVendor}=="09fb", ATTR{idProduct}=="6810", MODE="666"
Instalar Quartus 13 en Ubuntu de 64 bits (Ubuntu 16.04)
Quartus 13 es la versión que hace falta para trabajar con MiST pero hay partes del paquete que requieren librerías de 32 bits y hoy en día lo normal es tener instalada la versión de 64 bits del sistema operativo. En mi caso uso Ubuntu Mate 16.04. Para añadir las librerías de 32 bits adecuadas hay que ejecutar el comando:
apt install make:i386 libxdmcp6:i386 libxau6:i386 libxext6:i386 libxft-dev:i386 libxft2:i386 libxrender1:i386 libxt6:i386 libfontconfig1-dev:i386 libxtst6:i386 libx11-6:i386 unixodbc:i386 ncurses-base:i386 libzmq3-dev:i386 libxext6:i386 libxi6:i386
como root.
Ahí están casi todas las librerias. Falta alguna de las que la guía de instalación lista para ejecutar el simulador ModelSim, pero yo como habitualmente no lo uso no lo tengo puesto. De hecho, para usarlo es casi mejor preparar una máquina virtual con CentOS 6 en 32 bits pues ahí la instalación es más sencilla.
Entrevista en Retromaniac
Esta semana me han hecho una entrevista en Retromaniac enfocada a las FPGA y su papel en el mundo retro. Ha sido muy interesante poder explicar mi punto de vista de la escena en una publicación de calado. Aquí os dejo el enlace.
Instalar MPLAB-X IDE v3.60 en Ubuntu 16.04 (64 bits)
El MPLAB-X IDE es el entorno de desarrollo para lo famosos PIC de Microchip. Como este programa es para 32 bits, para instalarlo en un sistema operativo de 64 bits tenemos que tener algunas librerias de 32 bits instaladas. Las que pida concretamente dependerá de si ya tenías alguna instalada antes o no. A mí me ha pedido estas:
libc.so libdl.so libgcc_s.so libm.so libpthread.so librt.so libstdc++.so libexpat.so libX11.so libXext.so
Para encontrar el nombre del paquete que contiene cada archivo usamos la utilidad apt-file, que se instala desde el repositorio. Probando para cada nombre vamos recogiendo los nombres de paquetes hasta que por fin podemos formar el comando necesario para instalarlos todos:
sudo apt install libc6-i386 libx32stdc++6 libx11-6:i386 libxext6:i386 libexpat1:i386
Algunos paquetes no salen listados como i386 pero se pueden instalar añadiendo :i386 al nombre, como está hecho en el comando.
Después de instalar las librería ya puedes ejecutar el programa de instalación y todo irá bien.
El ancho de banda y por qué las recreativas eran mejores que los ordenadores
En los 80 y 90 se entendía la informática como algo bipolar: o tenías 8 bits o tenías 16 bits. Y esas palabras parecían contener toda la enjundia posible. Sólo con ese número se resumía por completo la capacidad de un equipo, ya fuera ordenador o consola. Sin embargo, esa no era toda la historia. Lo que todos ignorábamos era que esas máquinas de los bares y salones a menudo tenían una CPU de 8 bits y menos RAM que nuestros ordenadores… Incluso la Megadrive, consola de 16 bits, no estaba a la altura de las máquinas recreativas. ¿Qué pasaba?
Ghosts’n Goblins en máquina (8 bits), Atari ST (16 bits) y Amstrad CPC (8 bits)
Lo que pasaba se llama ancho de banda de memoría. Y consiste en que los ordenadores compartían la memoria entre los distintos componentes. Habitualmente dos: el procesador general (Z80 o motorola 68000) y el circuito de vídeo. Y si el procesador además llevaba la gestión de la música, podemos decir también que el chip de sonido entraba a compartir también el acceso a memoria.
Imaginaos: el procesador tenía que leer de la memoria lo que tenía que pintar, pintarlo en otra posición de memoria, leer también la siguiente nota a ejecutar y pasarla al chip de sonido y por supuesto tenía que leer el programa a ejecutar y escribir en memoria lo que estaba pasando con los personajes. Para más INRI, a veces el procesador iba a acceder a memoria y no podía, porque el circuito de vídeo le bloqueaba el acceso y tenía que pararse y esperar.
En las consolas el panorama era similar: todo (gráfico, juego y música) estaba grabado en un cartucho que tenía una conexión con la consola que formaba un cuello de botella porque cada componente de la consola competía por acceder al cartucho.
¿Pero y en los arcades? Bueno, pues estás máquinas alucinantes tenían desde el principio buses dedicados para cada función. El procesador del juego tenía su propia memoria que no compartía y a cuyo acceso no iba a verse bloqueado. Había otro procesador para la música con su propia memoria y además los circuitos gráficos accedían a las memorías ROM donde estaban los dibujos por buses independientes. Así que todo podía funcionar sin interferirse y a mucha más velocidad a pesar de que los componentes individuales fueran de 8 bits… y si encima eran de 16 bits, ni te cuento.
Esta historia viene a cuento del panorama FPGA actual. Los sistemas más activos actualmente son el ZX-UNO y el MiST y los dos se pensaron para replicar ordenadores domésticos así que sólo cuentan con una memoria y los componentes que se repliquen dentro de la FPGA han de compartir el acceso. ZX-UNO tiene una memoria de 8 bits y MiST tiene una de 16 bits. Los dos sistemas han demostrado que pueden hacer con éxito lo que nacieron para hacer: un ZX Spectrum y un Atari ST. Sin embargo, tienen en su diseño el cuello de botella de la memoria. Como estas memorias son más modernas es posible compartir su uso y aun así tener un rendimiento muy superior al de equipos de los años 80 y 90. Sin embargo, puede que recreativas de 8 bits como Gryzor, no puedan realizarse de forma fidedigna. Olvidaos ya de ver un Shinobi y una NeoGeo… ni te cuento.
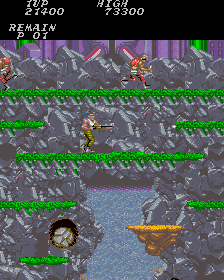
Gryzor (arcade, 8 bits)
Compilar iVerilog 10 en Ubuntu 16.04
Ubuntu viene con la version 0.9 de iVerilog. Para acceder a la última version hay que descargarla de aquí. Compilarla es sencillo: ejecutar ./configure y luego make. Pero la sorpresa puede venir cuando al ir a grabar en formato LXT iVerilog da un error:
LXT2 support disabled since zlib not available
En ese caso tenemos que instalar estas librerias:
sudo apt install libbz2-dev zlib1g-devy repetir la compilación: ./configure otra vez y luego make. Si os fijais en la salida del configure habrá unas líneas así:
checking for gzwrite in -lz... yes checking for gzwrite in -lz... (cached) yes checking for BZ2_bzdopen in -lbz2... yes checking for BZ2_bzdopen in -lbz2... (cached) yes
Comprueba que tengas un yes en todas ellas. Entonces la compilación producirá un iverilog capaz de generar LXT. Al final haz:
sudo make install
Y listo.
Entrevista en AmigaWave
El equipo de AmigaWave me entrevistó para su podcast/canal de youtube. Fue una charla interesante donde traté temas poco conocidos, como el esfuerzo que se está desarrollando para abrir chips antiguos y extraer el circuito original.
Os dejo aquí la entrevista en youtube, marcada ya en el minuto donde empieza.



Comentarios recientes